learnings
Programming
Data Structures
Arrays

Arrays

Definition and Characteristics

  • Linear Data Structure: An arråay is a collection of elements that are stored in contiguous memory locations.
  • Indexed: Each element in an array is identified by an array index, starting from 0 in most programming languages.
  • Homogeneous: All elements in a standard array are of the same type, which allows for efficient access to elements.

Types of Arrays

  1. One-Dimensional Arrays: The simplest form of an array, representing a linear sequence of elements. For example, [10]int; in Go declares an array of 10 integers.

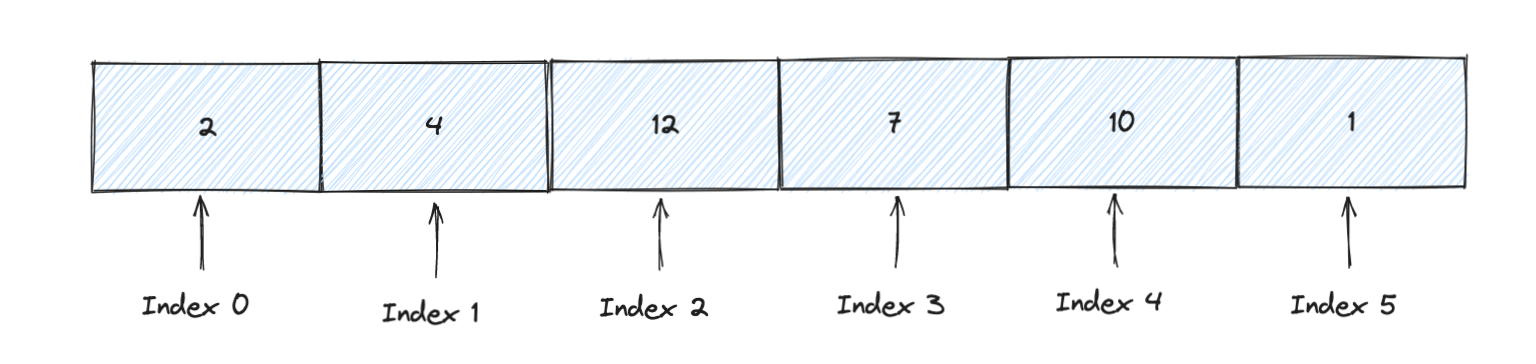
representation of an array

var myArray [6]int

myArray[0] = 2
myArray[1] = 4
myArray[2] = 12
myArray[3] = 7
myArray[4] = 10
myArray[5] = 1
graph TD;
    subgraph Array
    0((0)) --> A[2]
    1((1)) --> B[4]
    2((2)) --> C[12]
    3((3)) --> D[7]
    4((4)) --> E[10]
    5((5)) --> F[1]
    end
  1. Multi-Dimensional Arrays: Arrays with more than one level of indexing, commonly used to represent matrices or grids. For example, a 2D array can be declared as var matrix [3][3]int in Go. e.g.

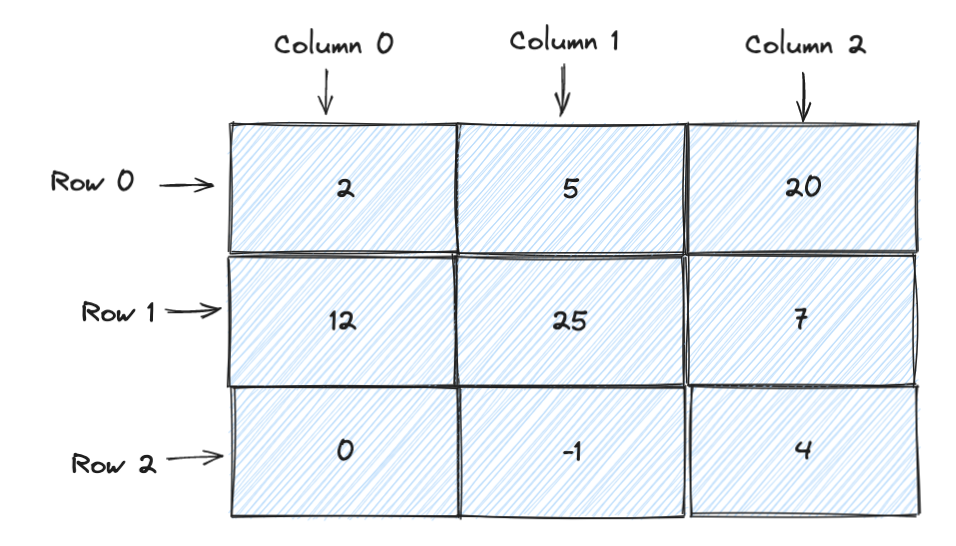
representation of a multidimentional array

    matrix = [3][3]int{
        {2, 5, 20},
        {12, 25, 7},
        {0, -1, 4},
    }
graph TD;
    subgraph Matrix
    00((0,0)) --> A[2]
    01((0,1)) --> B[5]
    02((0,2)) --> C[20]
    10((1,0)) --> D[12]
    11((1,1)) --> E[25]
    12((1,2)) --> F[7]
    20((2,0)) --> G[0]
    21((2,1)) --> H[-1]
    22((2,2)) --> I[4]
    end

Operations and Properties

Note that this table generally applies to simple, fixed-size arrays. Dynamic arrays (like slices in Go) might have different complexities due to resizing operations.

Operation Time Complexity Comments
Access O(1) Constant time due to direct indexing.
Search O(n) Linear search is O(n); however, if the array is sorted, binary search can be O(log n).
Insertion O(n) Inserting at the end is O(1) for dynamic arrays (amortized), but O(n) for fixed-size arrays due to shifting elements.
Deletion O(n) Deleting the last element is O(1), but O(n) for other positions due to shifting elements.
Appending O(1)* Generally, appending is O(1), but if a dynamic array needs to resize, it’s O(n). This is amortized O(1) over many append operations.
Size O(1) Determining the size of an array is a constant time operation.
Traversal O(n) Traversing all elements in an array is O(n).
  • Accessing Elements: Constant time operation (O(1)) because elements are stored in contiguous memory locations. Access is done via the index, like arr[3].
  • Insertion/Deletion: Generally not efficient in basic arrays as it involves shifting elements. This is an O(n) operation, where n is the number of elements in the array.
  • Size: In most static array implementations, the size is fixed and determined at the time of declaration. Dynamic arrays or vectors (like those in C++ STL or Java ArrayList) can adjust their size during runtime.

Advantages

  • Simplicity: Easy to understand and use.
  • Efficient Access: Due to contiguous memory allocation and indexing, reading elements is very efficient.
  • Cache Friendly: Due to contiguous memory usage, arrays make better use of CPU cache.

Disadvantages

  • Fixed Size: The size of static arrays is fixed, which can lead to either wasted space or insufficient capacity.
  • Poor Insertion/Deletion Performance: Requires shifting elements, which is inefficient for large arrays.

Applications

  • Used as the building block for many other data structures like heaps, hash tables, etc.
  • Efficient for scenarios where random access is more frequent than insertion/deletion.
  • Useful in algorithms that require sequential or fixed-size storage, like sorting algorithms.

Implementation Considerations

In many high-level programming languages, there are advanced versions of arrays with additional features. For instance, in Go, slices are a more flexible version of arrays that can grow or shrink in size. Similarly, in Python, lists are dynamic arrays that can grow or shrink in size. Similarly, in Java, the ArrayList class provides dynamic array implementation with more flexibility than a standard array.

Understanding arrays is foundational for delving into more complex data structures and algorithms, as they often underlie the implementation of these more advanced structures.

Data StructuresStrings